Periodicity and Harmonicity
A periodic signal has a harmonic spectrum. In the extreme case, a click train signal has a comb spectrum:
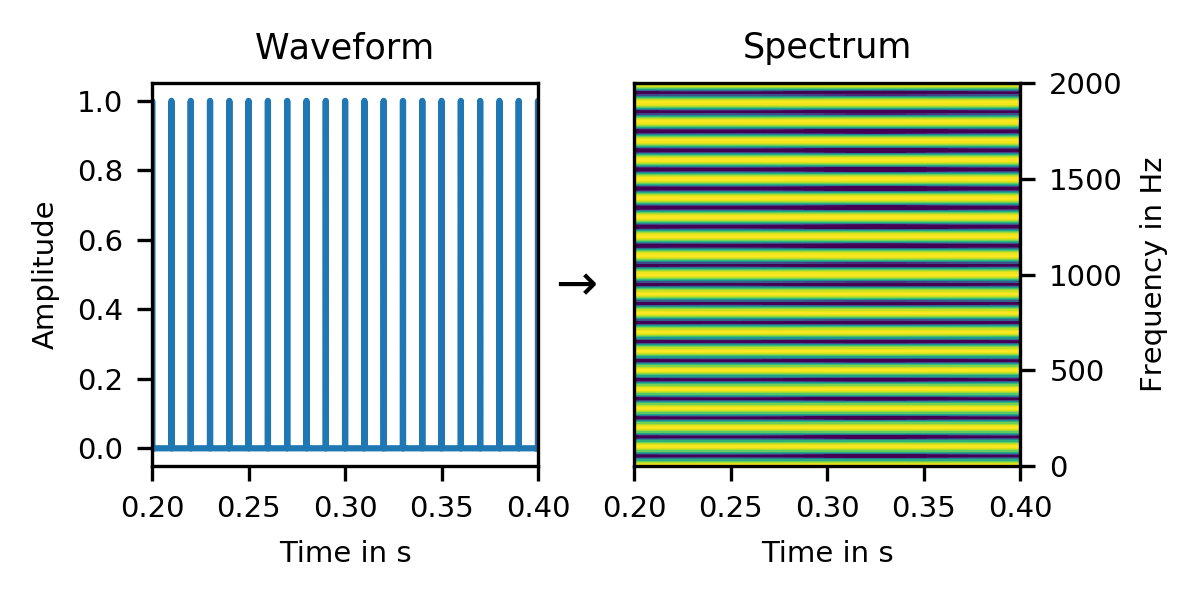
But why? After all, a solitary click has a uniform spectrum. So why should the sum of multiple clicks have a non-uniform spectrum?
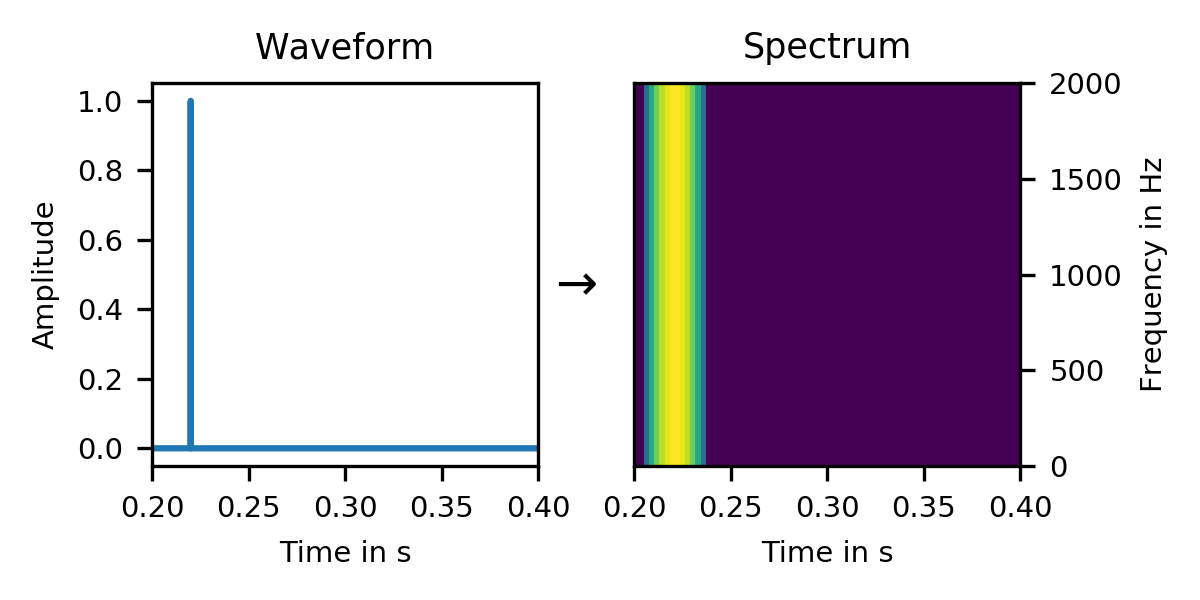
The answer exposes a lot of detail of how spectra work, and gives us a glimpse into the inner workings of spectral phases. Let's start with that click: In that spectrum, we see that we can decompose a click into a sum of sine waves:

As we have seen in the spectrum of the click earlier, it is composed of all frequencies (uniform spectrum). But we see here that the individual sine waves are delayed just so, that they all add constructively at exactly one time, and form the click. At all other times, they cancel each other out. This per-sine delay is called the phase of that frequency.
But what happens if we have more than one click? How does that change things?
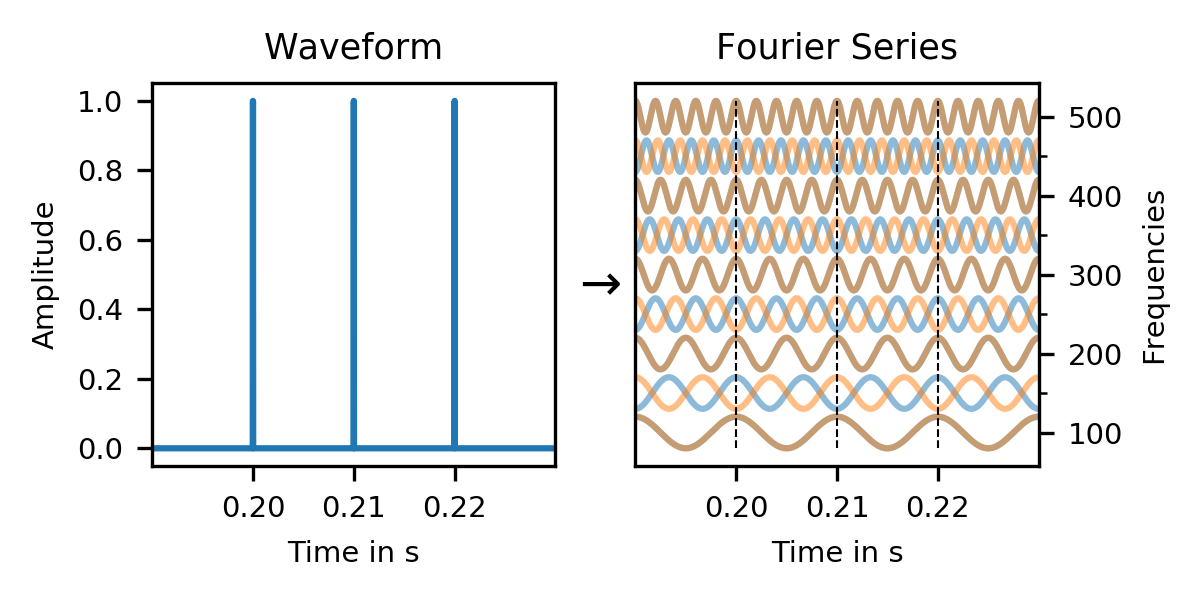
In a click train, odd frequencies in the Fourier series of the individual clicks cancel each other out (red/blue), and only harmonic frequencies (brown) remain. And this is exactly what our first spectrum showed: A periodic click train results in a harmonic spectrum.
Even though each click has a uniform spectrum, adding multiple clicks together cancels out all non-harmonic parts, and only a harmonic comb spectrum remains.
