20 Sep 2019

Analyzing Speech Signals in Time and Frequency

Our first stop in speech analysis is usually the short-time Fourier transform, or STFT¹:

Figure 1: Top: an STFT of speech (it's me, saying: "Es war einmal ein Mann"). Bottom: the signal's waveform.

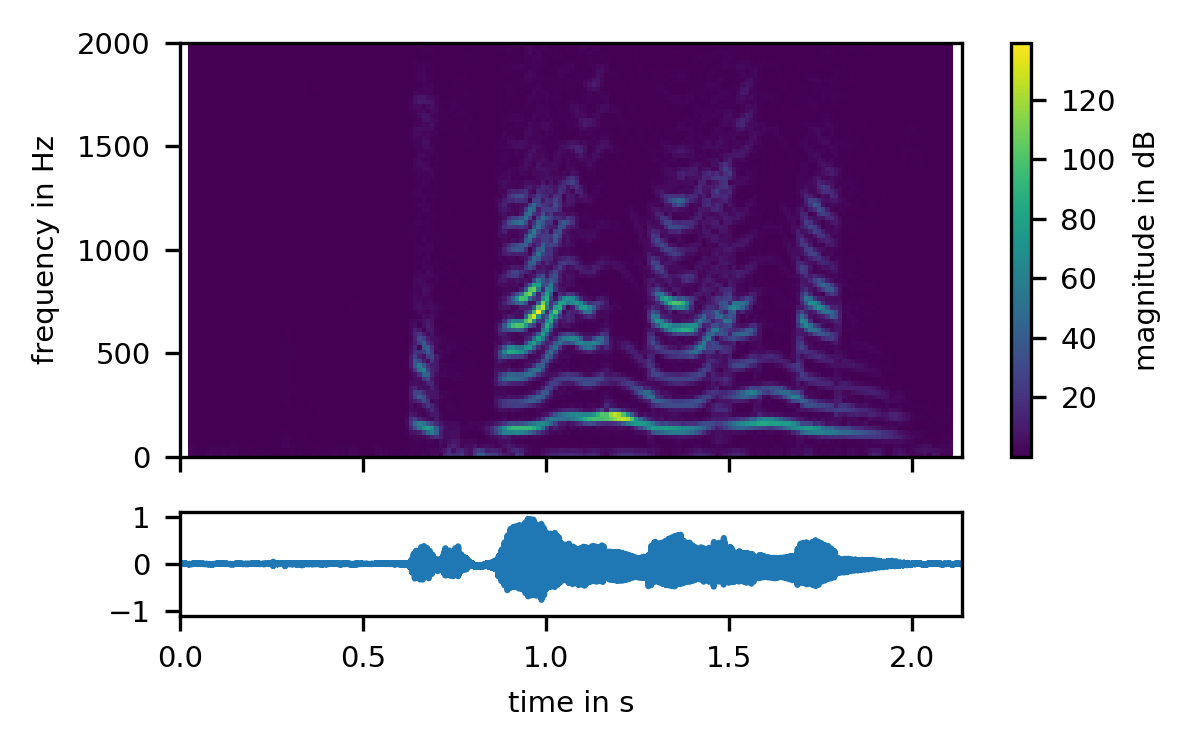
As we can see, this speech signal has a strong fundamental frequency track around 120 Hz, and harmonics at integer multiples of the fundamental frequency. We perceive the frequency of the fundamental as the speech's pitch. The magnitude of the harmonics varies over time, which we perceive as the sounds of different vowels.

All of this is clearly visible in this STFT. To calculate the STFT, we chop up the audio signal into short, overlapping blocks, apply a window function ² to each of these blocks, and Fourier-transform each windowed block into the frequency domain:

Figure 2: The STFT is a two-dimensional graph of short-time spectra. Window functions and corresponding spectra of some blocks are highlighted.

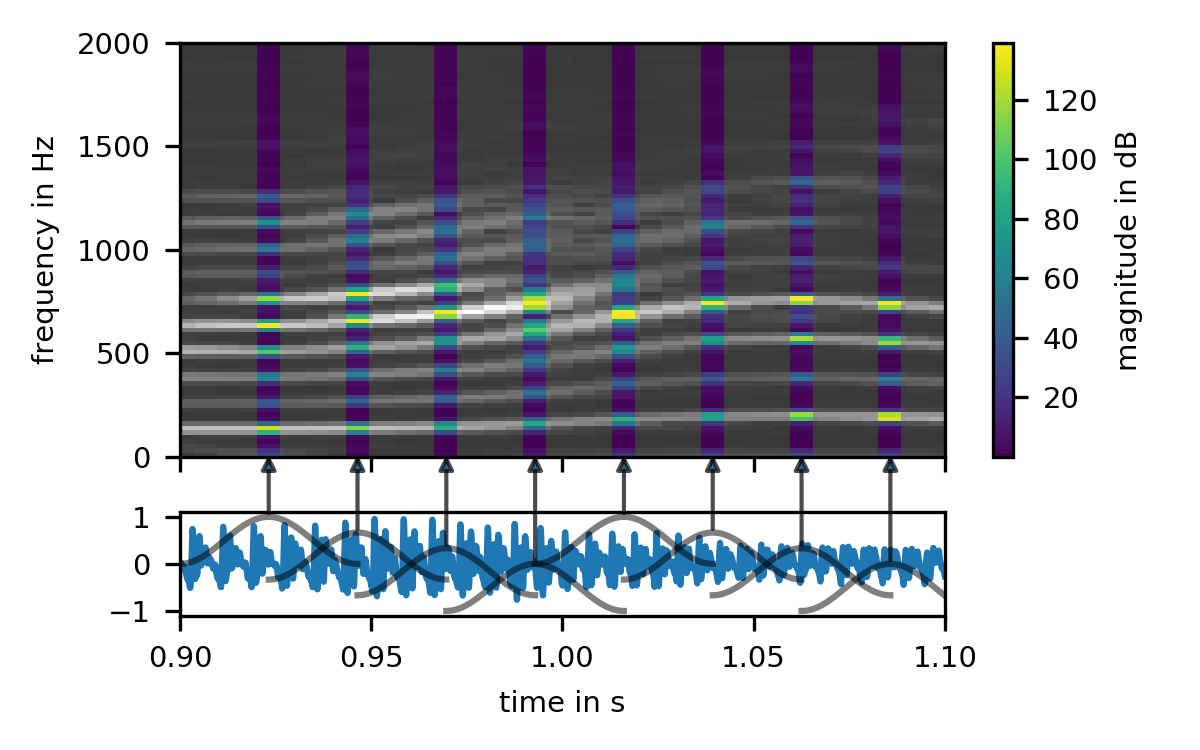
We zoomed in a bit to make this visible. At this zoom level, an old friend becomes visible in the waveform: The waveform of our harmonic spectra is clearly periodic. We also see that each of our blocks contain multiple periods of the speech signal. So what happens if we make our blocks shorter?

Figure 3: STFT with shorter blocks (graph shows a shorter time, too). Each window now covers roughly one period of the signal.

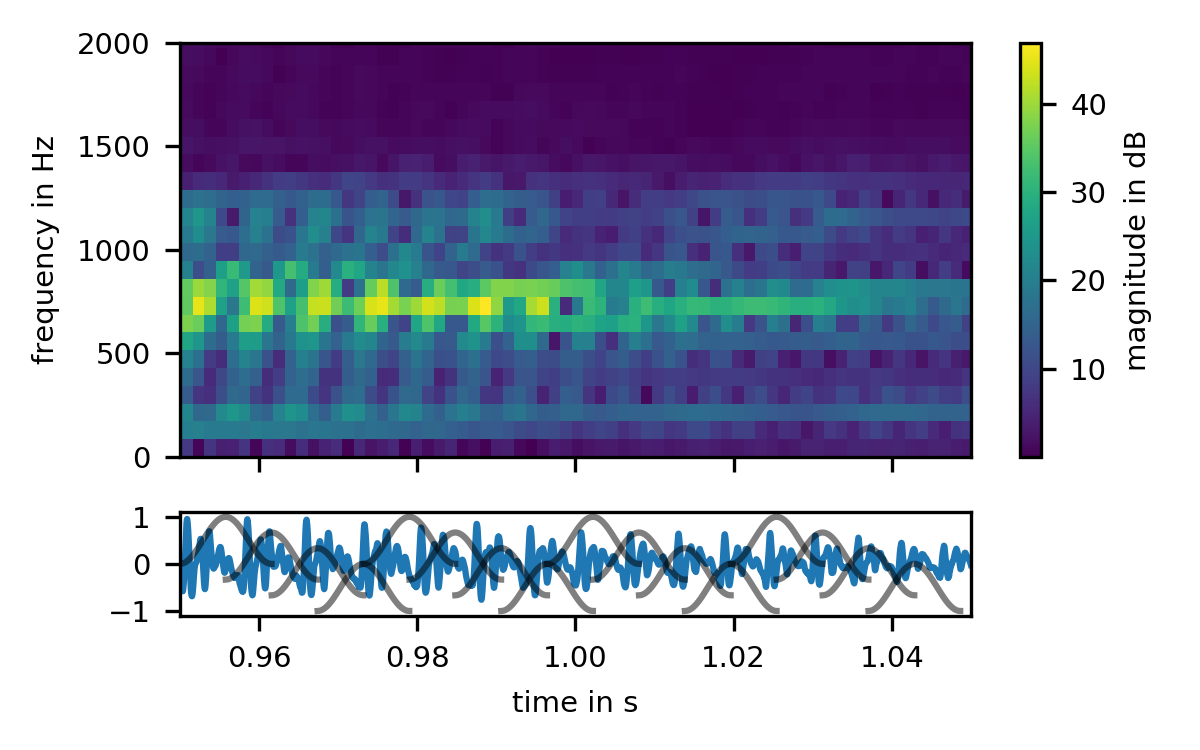
As we make our blocks shorter, such that they only contain a single period of the signal, a funny thing happens: the harmonic structure vanishes. Why? Because the harmonic structure is caused by the interference between neighboring clicks; As soon as each block is restricted to a single period, there is no interference any longer, and no harmonic structure.

But instead of a harmonic structure, we see the periodicity of the waveform emerge in the STFT! To look at this phenomenon in a bit more detail, we will have to leave the classical STFT domain, and look at a close sibling, the Constant Q Transform, or CQT. The CQT is simply an STFT with different block sizes for different frequencies:

Figure 4: The CQT uses shorter block sizes for higher frequencies and longer block sizes for lower frequencies.

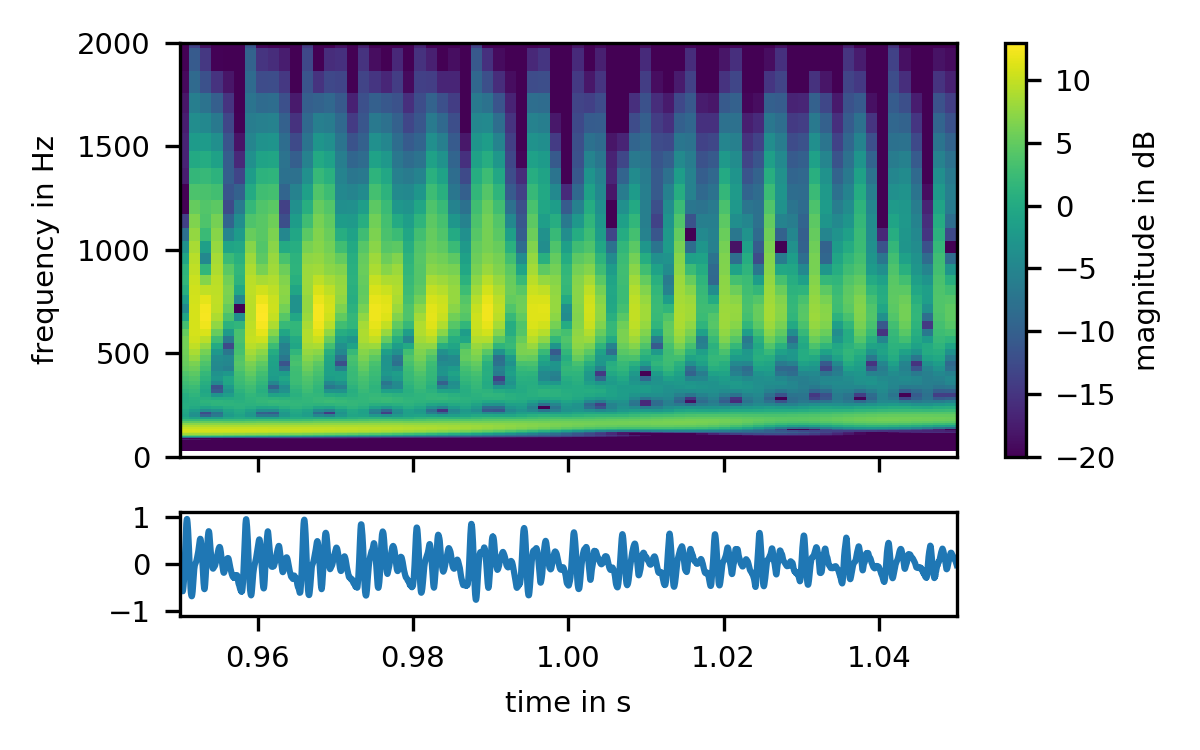
The periodic structure of the signal is now perfectly apparent. Each period of the signal gives rise to a skewed click-like spectrum that repeats at the fundamental frequency. Interestingly, however, the fundamental itself shows no periodicity. To see why this is so, and to finally get a grasp of how the short-time Fourier transforms interprets signals, we have to turn to our last graph, a gamma-tone filterbank:

Figure 5: A gamma-tone filterbank is a series of band-pass filters. Each horizontal line is now a frequency-constrained waveform.

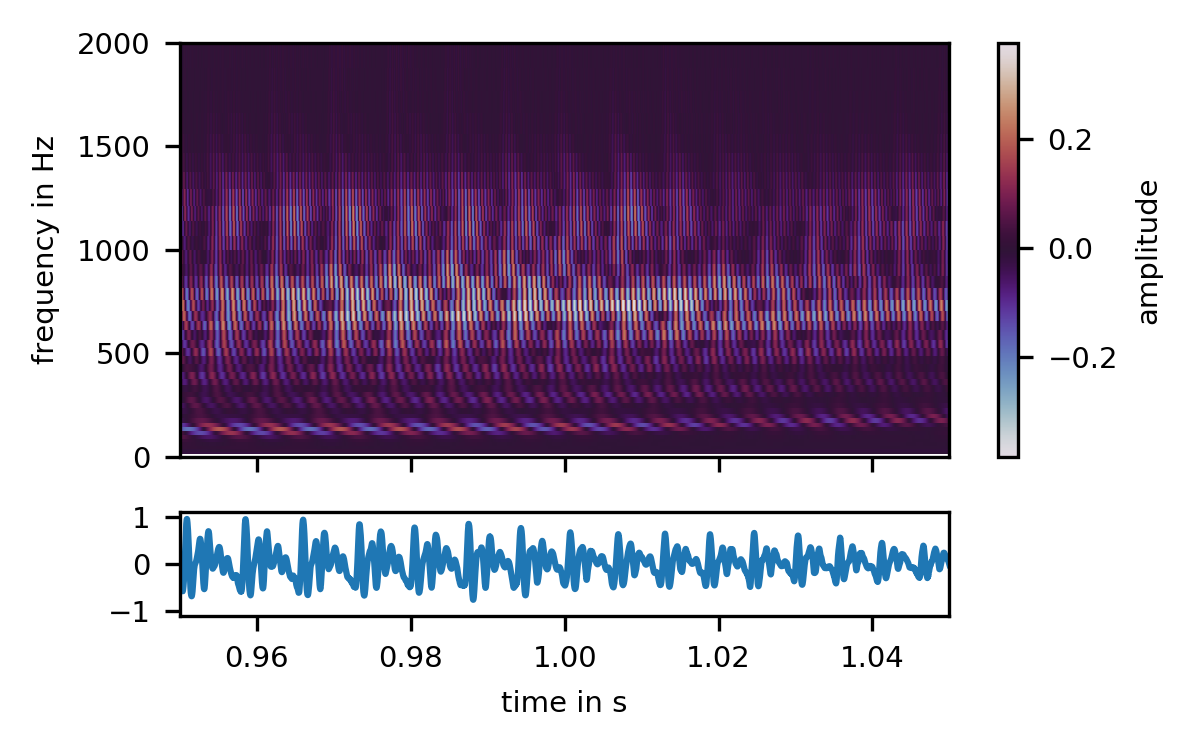
The fundamental frequency is now clearly a visible as a single sinusoid, rotating its merry way at 120 Hz. Each harmonic is its own sinusoid at an integer multiple of the fundamental frequency, but changing in amplitude in lockstep with the findamental. Thus in this graph, we see both the harmonicity and the periodicity at the same time, and can finally appreciate the complex interplay of magnitudes and phases that give rise to the beautiful and simple sound of the human voice³.

Footnotes:

also known as "spectrogram"

a Hann window, in this case

in the magnitude domain only; Phases, and different window functions, go beyond the scope of this article.